sinx/xの極限の証明

数学

どうもこんばんは、Jrです。

今回は\sin xの微分について説明した記事で解説できなかった、

    \begin{align*}\frac{\sin x}{x}\end{align*}

の極限がx \to 0で1になることの証明を行いたいと思います。

関連リンク：sinの微分ができないのは相当まずいよねって話

なお、この極限についても\sin xの微分同様、実際の計算ではいちいち定義に従って計算する必要はないと思いますが、一度は自力で証明してみることをおススメします。
証明を眺めて終わり…ではなく、自分の手を動かしてノートに証明を再現してみましょう。いずれ自分の力になります。

それではいってみましょう！

証明の方針：二つの面積ではさみこみを行おう

慣習として、角度は\thetaで表すことが多いので、以下では変数xを\thetaとさせてください。

\theta \to 0の極限を考えるので、\thetaの近づき方として、

  • 正の方向から近づく場合
  • 負の方向から近づく場合

の二通りを考える必要があります。
とりあえず考えやすいので、正の方向から近づく場合から考えましょう。

さて、基本的な方針としては、三角形の面積のはさみこみにより証明していきます。
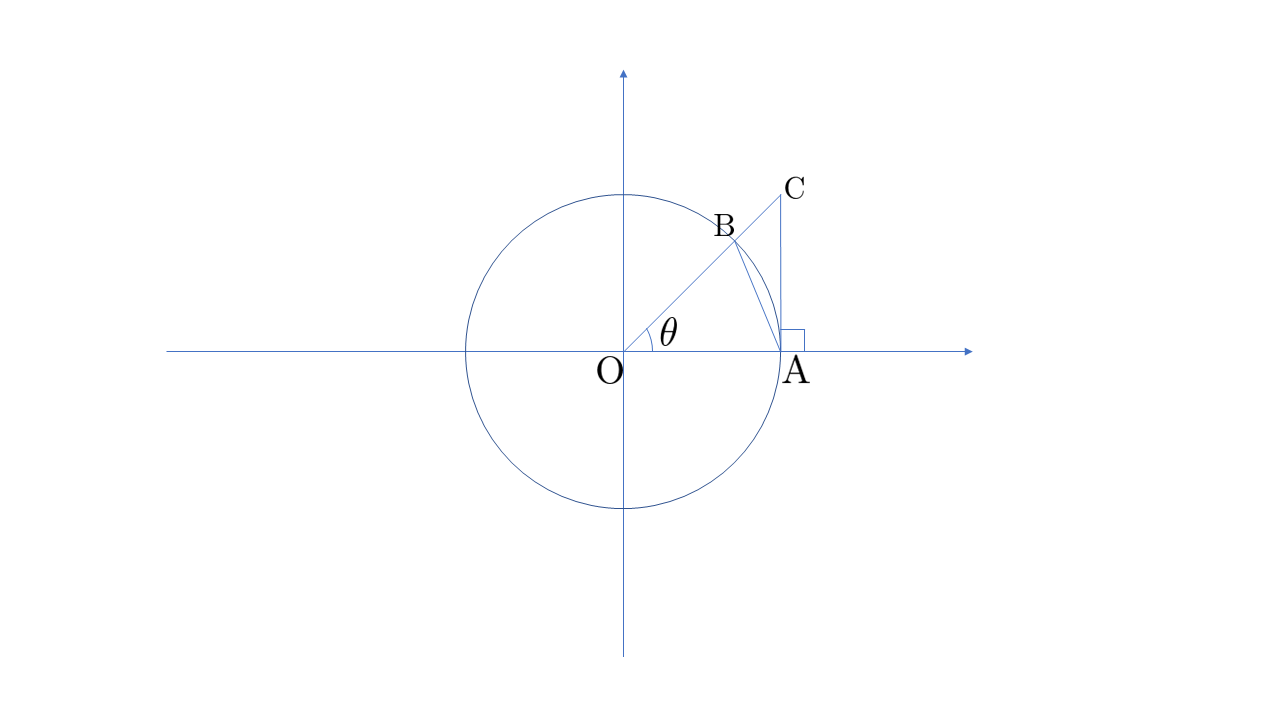
まずは以下の図を見てください。

図1. 証明に使う図

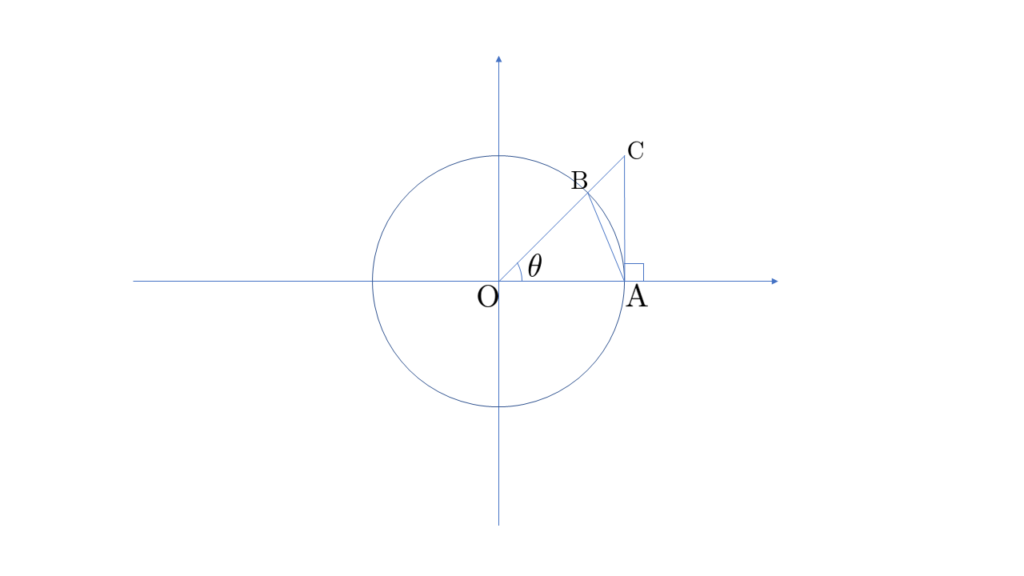
図が下手くそであるとか、パワポで作っててダサいとか、薄すぎるとかツッコミどころは満載ですがそれは置いておいて。

図1.の円は平面上の単位円とします。なお、単位円とは原点中心で半径が1の円を指します。
この図が非常に大切。

この図に現れる三つの図形

  • 三角形BOA
  • 扇形BOA
  • 三角形COA

に着目します。

まず、これらの図形の面積について、\thetaが正でかつ0に十分近いとき、

三角形BOAの面積<扇形BOAの面積<(直角)三角形COAの面積

が成り立ちます。
これらの面積を具体的に計算することで、はさみこむ事が出来ます。

三角形および扇形の面積の計算

続いてそれぞれの図形の面積を具体的に計算してみましょう。

三角形BOAの面積：

(1)   \begin{align*}\frac{1}{2} \sin \theta\end{align*}

これは三角形の面積の公式である(底辺)×(高さ)÷2をそのまま計算しただけです。なお、単位円であるから、半径が1であるという事実が利いています。

扇形BOAの面積：

(2)   \begin{align*}\pi \times \frac{\theta}{2 \pi} = \frac{\theta}{2}\end{align*}

これは単位円の面積\piと一周分の角度2\piに対する\thetaの比\theta/2\piの積により計算できます。

三角形COAの面積：

(3)   \begin{align*}\frac{1}{2}AC = \frac{1}{2} \tan \theta\end{align*}

これも三角形の面積の公式と\tan \theta = AC/OAにより計算しています。

不等式の構成、および証明

(1)(2)(3)より、

(4)   \begin{align*} \frac{1}{2} \sin \theta < \frac{\theta}{2} < \frac{1}{2} \tan \theta \end{align*}

が成立します。辺々2を掛け逆数を取ることで、

    \begin{align*}\frac{1}{\tan \theta} < \frac{1}{\theta} < \frac{1}{\sin \theta}\end{align*}

を得ます。さらに両辺に\sin \thetaを掛けることで、

(5)   \begin{align*}\cos \theta < \frac{\sin \theta}{\theta} < 1\end{align*}

ここで、

  • \cos \theta \to 1~(\theta \to +0)
  • 1 \to 1~ (\theta \to +0)

となるので、はさみうちの原理より

(6)   \begin{align*}\frac{\sin \theta}{\theta} \to 1~ (\theta \to +0)\end{align*}

を得ます。
これより\theta \to +0の場合が証明できました。

負の方向から近づく場合

実はこの場合も上記とほぼ同様の議論により

(7)   \begin{align*}\lim_{\theta \to -0} \frac{\sin \theta}{\theta} = 1\end{align*}

を示すことが出来ます。

これについては読者の方の宿題としてみたいと思います。良かったら是非考えてみてください。

(6)(7)を合わせることにより、

(8)   \begin{align*}\lim_{\theta \to 0} \frac{\sin \theta}{\theta} = 1\end{align*}

が示されました。

(証明終)

おわりに

というわけで今回は\sinに関する有名な極限を証明してみました。結果は有名だし、やり方を言われれば簡単だけど、意外とそらで証明しようとすると躓いてしまう人も多いのではないでしょうか？

覚えておく必要はないですが、この機会に一度自分で証明してみるのもいいかもしれませんね。

今回はできていませんが、大学の数学とのつながりを意識して数学ネタを書けたら、書いている自分としても楽しそうだし、約に立つ記事にもなるのかなーと思ったり。
あるいは自分がどうやって理解しているかを解説したりするのも面白そう。

そんな感じで数学に関する記事も増やせれば楽しいかなーと思っています。

それではまた別の記事でお会いしましょう。

コメント

タイトルとURLをコピーしました