どうもこんばんは、Jrです。
少し前に、後輩が

SIRモデルを用いて感染症のシミュレーションを行うの楽しいですよ
と言っていたのを思い出して自分でもやってみたところ、接触を控えることが思った以上に感染拡大の本質に関わってくるのかもしれないということがわかってきたので、記事にしてみました。
ここで言う「面白い」とは「興味深い」の意味であり、愉快といったニュアンスではないことを注意しておきます。
なお、本記事を作成するにあたり、JBpressさんのこちらの記事を大いに参考にさせていただきました。
また、本記事の結果はあくまでもいくつかの仮定を基にしたシミュレーションなので、実際の問題を再現しているものではないことを述べておきます。
あくまでこういった傾向にある…といった理解でお願いします。
SIRモデルとは
まずSIRモデルについての情報をWikipediaより引用しておきます。
SIRモデル(エスアイアールモデル)は、感染症の短期的な流行過程を決定論的に記述する古典的なモデル方程式である。名称はモデルが対象とする
感受性保持者(Susceptible)
感染者(Infected)
免疫保持者(Recovered、あるいは隔離者 Removed)
の頭文字にちなむ。
https://ja.wikipedia.org/wiki/SIR%E3%83%A2%E3%83%87%E3%83%AB
要するに感染症を記述する数理モデルと言えるかと思います。
具体的には以下の様に三本の連立した常微分方程式系により表されます。
(1) 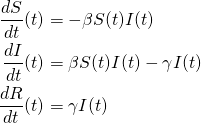
ここで、![]() はそれぞれ感受性保持者(感染するかもしれない人)、感染者、免疫保持者(回復した人)の人数を表します。
はそれぞれ感受性保持者(感染するかもしれない人)、感染者、免疫保持者(回復した人)の人数を表します。
また、![]() はそれぞれ感染率、回復率を表し、
はそれぞれ感染率、回復率を表し、![]() の逆数は平均感染期間を表します。
の逆数は平均感染期間を表します。
このシステムの大きな特徴として、(1)の三式の和を取ると0になるということがあります。つまり、
(2) ![]()
が成立します。これは人口に関して保存則が成立することを意味しています。
言い換えれば、時間変化で総人口が変化しないということを仮定しているとも言えます。
他にも基本再生産数など重要な概念があったり、このシステムに関する解析も色々となされているようですが、今回はシミュレーションをしてみたいだけなので、詳細は省略します(というか実は自分もよく知らない)。
数値計算によるシミュレーション
さて、具体的なパラメータと初期値を与えると実際に(数値計算により)解くことが出来ます。
で、問題はパラメータをどのように与えるかということで、本当はコロナウイルスの感染率や回復率を利用したかったのですが、イマイチわからなかったので適当に仮定することにしました。
接触を控えることによる感染の様子の変化をシミュレートするには、正確な感染率や回復率が必ずしも必要ではなかったりもします。
このことはこの記事を読んで気づいたのですが、目からうろこでした。
ということで、まずは具体的なパラメータを定めてみます。まずは回復率から。
感染期間を14日と仮定してみると、![]() となります。
となります。
次に、感染率![]() ですが、これは一回の接触当たりの感染率ということなので、一人が一日に接触する人数の平均を
ですが、これは一回の接触当たりの感染率ということなので、一人が一日に接触する人数の平均を![]() 、それぞれの接触により感染が生じる確率を
、それぞれの接触により感染が生じる確率を![]() 、総人口を
、総人口を![]() としたときに
としたときに
(3) ![]()
により決定されるとのこと。
まずは![]() と仮定してみます。なお、
と仮定してみます。なお、![]() についてはこちらの記事を、
についてはこちらの記事を、![]() については東京都のサイトを参考に適当に四捨五入をして決定しました。
については東京都のサイトを参考に適当に四捨五入をして決定しました。
次に初期値を設定します。それぞれ以下の様に決定しました。
1519というのは4/9における東京都のコロナウイルスの陽性反応者数の累計です(東京都の発表を利用しました)。
本当は退院者や死亡者を考慮して![]() も考慮したほうが良いのでしょうが、今回は簡単のため0としました。
も考慮したほうが良いのでしょうが、今回は簡単のため0としました。
この仮定の下、pythonを用いて数値計算を行った結果が以下の図になります。
ここで横軸が日数、縦軸が人数を表しており、青、赤、緑の線はそれぞれ
- 感受性保持者
- 感染者
- 免疫保持者
を表します。
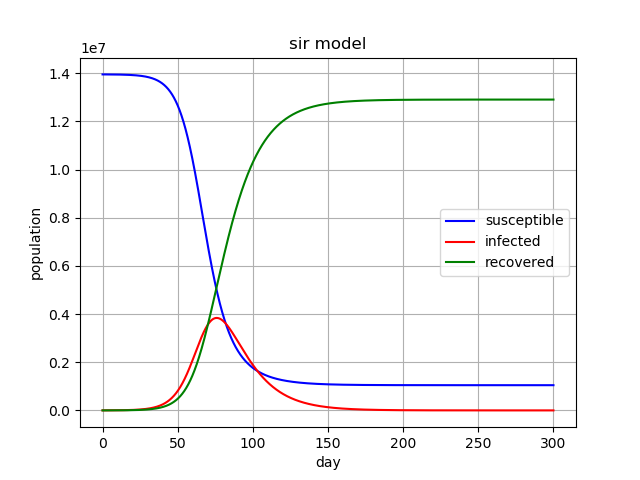
次に![]() を減らして
を減らして![]() として同様の計算を行ってみます。
として同様の計算を行ってみます。
グラフの概形は同じですが、ピークに至る時刻、およびピーク時の感染者数が減っていることがわかります。
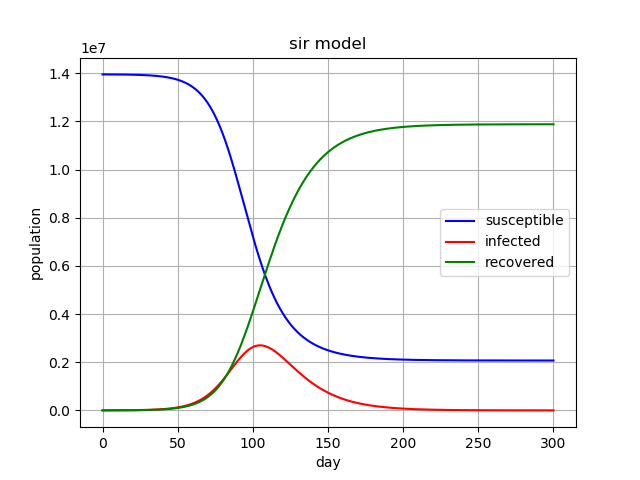
同様に![]() の場合も計算を行ってみます。
の場合も計算を行ってみます。
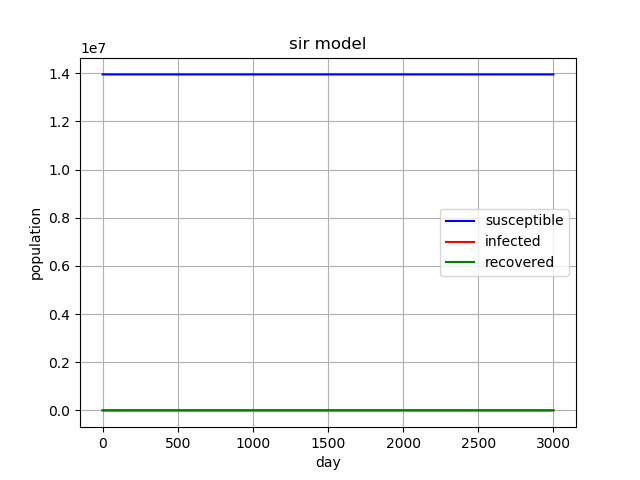
![]() の場合はグラフの概形が全く違いますが、これは流行が起こらないことを意味します。
の場合はグラフの概形が全く違いますが、これは流行が起こらないことを意味します。
ただこの場合はそもそもとしてパラメータが適切ではないのかもしれません。
接触を控えることによる感染の変化
さて、計算結果のグラフからわかることがいくつかあります。
一つ目が![]() を小さくする、すなわち接触を控えることにより感染者数を減らすことができること。
を小さくする、すなわち接触を控えることにより感染者数を減らすことができること。
二つ目が接触を控えることにより感染のピークが起きる時期を遅らせることが出来るということです。
一つ目に関しては文句なしに良いことですね。感染者数が少なく済むのですから。
二つ目に関しては一見するとピークが遅れるだけで結局流行が起きてしまうので意味がないのではないか?と感じるかもしれません。
ですが、ピークが遅れるということはそれだけウイルスについて調べることが出来る時間があるということでもあり、その間に特効薬や有効な対策を用意できるかもしれません。
そういった意味でも、ピークを遅らせることは有意義であると考えられます。
これらのことから、接触率を減らすことは感染拡大を防ぐ非常に有効な方法であるのではないかと思います。
もちろんSIRモデルは簡略化されたモデルであるし、今回設定したパラメータはあくまでこちらで与えたものなので必ずしも実現象を再現しているわけではありません。
ですが、対策として有効であることは変わらないと思います。
計算に用いたソースコード
本記事の計算では以下のコードを用いました。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
def sir(u,t,b,g):
S = -b*u[0]*u[1]
I = b*u[0]*u[1] -g*u[1]
R = g*u[1]
return [S,I,R]
b = (10*0.02)/13950000
g = 1.0/14.0
u0 = [13950000-1519,1519,0.0]
t = np.arange(0.0,300,0.001)
args = (b,g)
r = odeint(sir,u0,t,args)
fig,ax = plt.subplots()
ax.set_xlabel('day')
ax.set_ylabel('population')
ax.set_title('sir model')
ax.grid()
c1,c2,c3 = "blue","red","green"
l1,l2,l3 = "susceptible","infected","recovered"
ax.plot(t,r[:,0],color = c1, label = l1)
ax.plot(t,r[:,1],color = c2, label = l2)
ax.plot(t,r[:,2],color = c3, label = l3)
ax.legend(loc=0)
plt.show()
#plt.savefig('sir10.png')
bの定義中の10が平均接触人数を表すので、ここを適当に変えれば色々と結果が変わります。
おわりに
SIRモデルを用いたシミュレーションを行ったことで、接触を減らすことが感染拡大を抑えるカギになっていることを確認しました。
実際に自分で手を動かしてコードを書いて計算をしたことで、よりリアリティを感じることが出来たと思います。
なので、プログラムが書ける人は一度自分でコードを書いて実行してみるといいかもしれません。
ソースコードは自分で書きましたが、 結果としてJBpressさんのこちらの記事の再実験に近い記事になってしまいました。
問題などがありましたら、お知らせください。
それではまた別の記事でお会いしましょう。











コメント