おはようございます、Jrです。
以前(もうかなり前)に![]() と
と![]() の微分を定義から計算してみよう、といった旨の投稿をしました。
の微分を定義から計算してみよう、といった旨の投稿をしました。
今回は今更ながらその続きとなる記事で、最後の三角関数![]() の微分を計算してみよう!という記事になります。
の微分を計算してみよう!という記事になります。
定義に戻って一つずつ計算するだけですが、式変形が長くて少し手こずるかもしれません。
と言っても、![]() や
や![]() の加法定理や、三角関数間の関係式をきちんと理解していればきっと計算できると思います。
の加法定理や、三角関数間の関係式をきちんと理解していればきっと計算できると思います。
高校生の方や、計算が合ってるか不安な人は、続きを読む前にまずは一度自分で計算してみるといいと思います。
では早速計算していきましょう!
微分の定義
まずは微分の定義を与えておきます。以下で与える定義は、いわゆる微分係数の定義です。
![]() を実数から実数への連続写像とする。このとき、次の極限
を実数から実数への連続写像とする。このとき、次の極限
![]()
が存在するとき、![]() は
は![]() で微分可能であるという。
で微分可能であるという。
この極限を![]() の
の![]() における微分係数と呼び、
における微分係数と呼び、![]() などと書く。
などと書く。
実は上の定義は少し曖昧な部分もあったりするのですが、とりあえずここでは上の極限を微分と呼ぶことにします。
厳密な定義を知りたい人は、教科書や参考書を読んでみましょう。
なるべく正確に記述することを心がけてはいますが、間違えたことを書いてしまうこともあるかもしれないので、やはり教科書に戻って確認するのは大切です。
たまに教科書も間違えてたりするから困っちゃうけどね。特に大学の教科書は普通に誤植が良くあったりします。
必要となる関係式
次に、![]() の微分を計算するのに必要な関係式を4つほど挙げておきます。
の微分を計算するのに必要な関係式を4つほど挙げておきます。
![]()
一つ目は![]() と
と![]() を結ぶ関係式で、非常に重要です。これはしっかり覚えましょう。
を結ぶ関係式で、非常に重要です。これはしっかり覚えましょう。
一見良くわからないかもしれませんが、三角形の比として三角関数を理解していれば、この関係式が自然に感じられると思います。
![]()
これもかなり重要な関係式になります。
こちらに関しては、単位円と三角関数の関係が理解できていれば、ただ三平方の定理を三角関数を使って示しているだけである、ということがわかると思います。
最後に残り二つの関係式を挙げます。
![]()
![]()
この二つも非常によく使う定理なので、さらっと答えられるようにしておくといいと思います。
もちろん、この二つの式についても導出が出来るはずなのですが、お恥ずかしながら導出の仕方を忘れてしまいました。
復習しておくので、いずれ記事にしたいと思います。
また、![]() の加法定理に関しては良く符号を間違えがちなんですが、これに関してはおススメの確認方法があります。
の加法定理に関しては良く符号を間違えがちなんですが、これに関してはおススメの確認方法があります。
それは、![]() として加法定理を計算してみるという方法です。
として加法定理を計算してみるという方法です。
実際この設定であえて符号を間違えて計算すると、
![]()
となります。
これはどんな角度![]() を持ってきたとしても、その二倍の角度に関しては
を持ってきたとしても、その二倍の角度に関しては![]() の値が1になる、ということを主張した式になりますが、そんなわけないですよね。
の値が1になる、ということを主張した式になりますが、そんなわけないですよね。
例えば、この式を用いると![]() となりますが、正しくは
となりますが、正しくは![]() なので、こんな感じですぐに反例が作れます。
なので、こんな感じですぐに反例が作れます。
ということは加法定理が間違えていたということになり、符号が逆なんだな、といった感じに正しい符号が思い出せます。
この確認方法を使うには符号以外の部分については加法定理をしっかりと覚える必要がありますが、そこは頑張って覚えましょう!
というより使っているうちに自然に覚えると思います。
以上で準備はできたので、これから実際に微分の計算をしてみましょう。
具体的な微分計算
ここからはひたすら計算をしていきます。
記事の冒頭で計算をした人は自分の計算と見比べながら、わからなかった人は以下の計算を自分でも一度しながら読むといいと思います。
まず定義から
(1) ![]()
です。ここからは式が長くなるので分子だけ取り出して変形をしていきます。
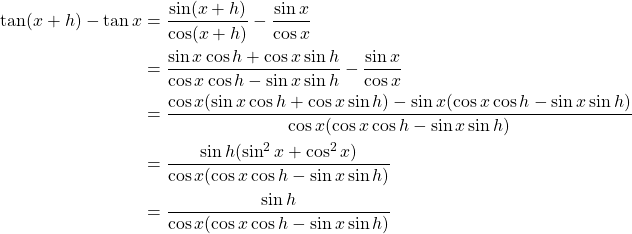
式変形の解説をしていきます。
まず初めの等式では、関係式1を用いて![]() を
を![]() により表しています。
により表しています。
二番目の等式で、第一項を加法定理を用いて分解し、次の等式で通分をしています。
分子が![]() でくくれることに着目して因数分解を行い、最後の等式で関係式2を用いています。
でくくれることに着目して因数分解を行い、最後の等式で関係式2を用いています。
さて、ここまでくればあともうちょっと!
この式を(1)に代入して極限計算を行っていきます。
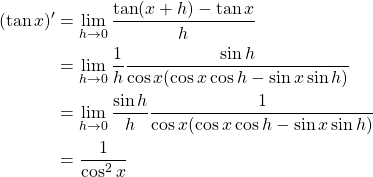
最後の方は少し省略してしまっていますが、こんな感じで変形が出来ます。
ざっくりと説明すると、まず最初は代入しただけですね。
で、次の等式で![]() の形を作ります。理由としてはこの極限が1になるからですね。
の形を作ります。理由としてはこの極限が1になるからですね。
ちなみにこの極限が1になることについては、別の記事で書いているのでそちらも参考にどうぞ。
そして最後に![]() と
と![]() を用いました。
を用いました。
これで無事![]() の微分が定義通りに計算できました。めでたしめでたし。
の微分が定義通りに計算できました。めでたしめでたし。
ただ、![]() や
や![]() と違って、
と違って、![]() は微分できない点があることには注意が必要です。
は微分できない点があることには注意が必要です。
というのも![]() は
は![]() で定義できなくなってしまい、その時は微分の定義に現れる極限が確定せず微分が不可能になります。
で定義できなくなってしまい、その時は微分の定義に現れる極限が確定せず微分が不可能になります。
何故これらの点で![]() が定義できないかについては、関係式1にこれらの角度を代入してみるとわかると思います。
が定義できないかについては、関係式1にこれらの角度を代入してみるとわかると思います。
例えば![]() を代入すると、
を代入すると、
(2) ![]()
となりますが、ここで![]() は0です。したがって、(2)の右辺に0割が表れてしまい、定義ができなくなるというわけです。
は0です。したがって、(2)の右辺に0割が表れてしまい、定義ができなくなるというわけです。
こんな感じで定義が出来なくなる点を特異点と言ったりします。
実は特異点という言葉の厳密な定義はよくわかっていないので、調査しておきます。
最後に![]() の微分を改めて公式として書いておきます。
の微分を改めて公式として書いておきます。
![]()
まとめ
ということで、長らく放置してしまっていた三角関数を定義通りに計算してみようシリーズ最終回として、![]() の微分を定義通りに計算してみました。
の微分を定義通りに計算してみました。
定義に戻って微分計算を計算することって中々ないとは思いますが、一度はやってみるべきなので、やったことがなかった人にとってはいい機会になったんじゃないでしょうか?
自分としても、改めて計算してみると割と面白かったです。
今後は別の関数、例えば指数関数とかの定義通りの計算について触れてもいいですし、せっかく三角関数のお話をしてきたので三角関数の応用について書いたりしても面白いなって思っています。
こういう話題について書いてほしい!とかっていうのがあれば、書ける範囲で書いてみようと思うのでコメントなど頂けると幸いです。
ではまた!








コメント