sinの微分ができないのは相当まずいよねって話

数学

どうもこんにちは、Jrです。

今回はタイトルの通りなのですが、\sinの微分に関する話題になります。
と言っても、特に難しい話をするわけではなく、高校の微積分の内容にしか触れないので、良かったら読んでいただけたら幸いです。

定義に基づいた\sinの微分の計算を書いたので、高校生の方の役にも立つかと思います。

それではいってみましょう！

ことの発端

ことの発端は非常に優秀な後輩のI君と話していた時のこと。

彼は指導教員の転勤の関係で、この春から某私立大学の博士課程への進学が決まっています。

その時のI君と自分との会話が大体以下の様な感じ。

I君
I君

(進学する)私立大学、\sinの微分ができない人がチラホラいるらしいですよ

Jr
Jr

いやそれは流石にやばいでしょw

ちなみに彼が進学する大学は、私立大の中でも相当有名なところなので割と本当にびっくりしたことを覚えています。
まあもしかしたらうちの大学の学生にも\sinの微分できない人いるかもしれませんけどね…。

彼曰く、推薦で入る人も結構多いし、国立よりも上下の差が激しいとのこと。

まあそんなことはともかくとして。
実際問題、\sinの微分ができないのってかなりやばいと思うんですよ。

当然自分は微分の結果は知っているんですが、そういえば定義に基づいて計算するとどうなるんだっけ？と思って計算したら、少しだけ悩んでしまったんですね。

で、これはまずいだろうと思ったので、反省の意味も込めてこの記事を書くに至りました。

微分の定義

まずそもそもとして、関数の微分の定義について簡単に復習したいと思います。

実数から実数への連続関数f(x)を考えます。
記号では、f:\mathbb{R}\to\mathbb{R}などと書いたりします。

このとき、関数fのxによる微分とは

    $$\frac{df}{dx} = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$$

により定義されます。

左辺がfをxで微分するよっていう記号で、実際の定義式が右辺となります。
ちなみに微分の記号は\frac{df}{dx}以外にもいくつかあって、例えばf'(x)と書いたりもします。

また、ここでいう微分とは導関数を表すものとします。

sinの微分：公式を使って

先ほど書いたのが微分の定義なのですが、基本的な関数、具体的には多項式からなる関数や三角関数、指数関数、対数関数なんかはいちいち定義に従って計算せず公式として覚えておりパパっと計算する人がほとんどだと思います。

覚えているといっても、公式として暗記するぞ！っていうより、どちらかというと身体に染みついている感じかと思いますが。めちゃくちゃよく使う関数たちなので。

ということで多くの理系の方は、\sin xの微分は？と聞かれたら計算せずとも\cos xと答えられるはずです。
受験生の方も一瞬で答えられるようにしておきましょう。答えられなかった人も、きちんと勉強しておけばいずれ身体に染みつくはずなのであまり気にしなくてもOK。

ということで、\sin xの微分についてまとめておくと、

    $$(\sin x)' = \cos x$$

となります。

sinの微分：微分の定義に従って

さて、上で見たように、\sinの微分はいちいち計算しなくてもパッと答えられるようにしておくべきではあるのですが、敢えて微分の定義に従って計算してみます。
ちなみに、普段の計算では公式的にパッと計算していいと思いますが、一度は定義に従って計算してみることをお勧めします。

これは微分に限った話ではなく、数学全般に言えることですが、一度自分で計算したり証明してみたりすることは自分の経験値として必ず役に立ちます。
自分は割と証明はサラッと読んだりすることが多かったため、研究室に入ってから苦労しました。今も苦労することは多いです。

ということで実際に計算してみましょう。

    \begin{align*}(\sin x)' &= \lim_{h \to 0} \frac{\sin (x+h) - \sin x}{h} \\&= \lim_{h \to 0} \frac{\sin x \cos h + \cos x \sin h - \sin x}{h} \\&= \lim_{h \to 0} \frac{\sin x (\cos h - 1) + \cos x \sin h}{h} \\&= \sin x \lim_{h \to 0} \frac{\cos h -1}{h} + \cos x \lim_{h \to 0} \frac{\sin h}{h} \\&= \sin x \lim_{h \to 0} \frac{(\cos h -1) (\cos h + 1)}{h(\cos h + 1)} + \cos x \lim_{h \to 0} \frac{\sin h}{h} \\&= \sin x \lim_{h \to 0} \frac{- \sin^2 h }{h (\cos h + 1)} + \cos x\\&= -\sin x \lim_{h \to 0} \frac{\sin h}{h} \frac{\sin h}{\cos h + 1} + \cos x \\&= \cos x\end{align*}

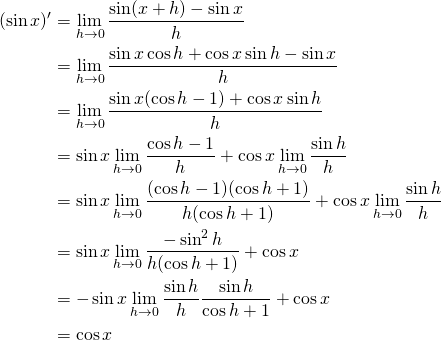
なお、計算の途中では三角関数の加法定理と

(1)   \begin{align*}\lim_{h \to 0} \frac{\sin h}{h} = 1\end{align*}

を使っています。これらについては、また別記事で解説しようと思います。

このように、定義から計算してもしっかりと公式と同じ結論を得ることができます。まあ当然ですね。

ちなみに、自分が悩んでしまったのは、(1)の極限が1になることの証明です。
これについても結果は知ってたしはさみうちで証明できることは覚えてたんですけど、何ではさみこむのかをパッと思い出せなかったんですよね…。不甲斐ない…。

おわりに

ということで今回は\sinの微分を定義に基づいて計算してみた記事でした。

本当は\sin x / xの極限についても解説したかったんですが、長くなってしまったので別の記事で解説したいと思います。

ではまた別の記事でお会いしましょう。

コメント

タイトルとURLをコピーしました