どうもこんばんは、Jrです。
少し久しぶりの数学関連の話題になります。
以前の記事で![]() の微分を定義に基づいて計算しました。今回は同じ三角関数の微分と言うことで、
の微分を定義に基づいて計算しました。今回は同じ三角関数の微分と言うことで、![]() の微分を定義に基づいて計算してみようと思います。
の微分を定義に基づいて計算してみようと思います。
なお、![]() の微分に関する記事はこちらになります↓
の微分に関する記事はこちらになります↓
![]() の微分に関しても、実際の計算では結果をそのまま公式的に使うことが基本で、定義に基づいて計算をする場面はあまりないと思います。
の微分に関しても、実際の計算では結果をそのまま公式的に使うことが基本で、定義に基づいて計算をする場面はあまりないと思います。
ですが微分の定義を理解するいい練習問題だと思うので、一度は自分で計算してみるのもいい経験になると思います。
では計算をしていきましょう。
問題:(cosx)’を定義に基づいて計算せよ
次の微分を「定義に基づいて」計算する問題を考えます。
![]()
ここで、![]() は
は![]() による微分を表すものとします。
による微分を表すものとします。
なお、有名な事実(公式)として、![]() の微分は
の微分は
![]()
であり、これは覚えてしまった方がいいです。と、言うよりも、練習問題を繰り返している間に勝手に覚えてしまうと思います。
今回の問題では、定義に基づいて同じ結果を導いてみましょう。
証明
この証明においても本質的となるのは加法定理と![]() に関する微分、
に関する微分、
(1) ![]()
の二つです。
まず、微分の定義から、
(2) 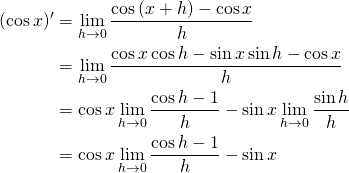
となります。ここで、2行目への変形で加法定理を、4行目への変形で(1)式を用いています。
さて、残っている項について、
(3) 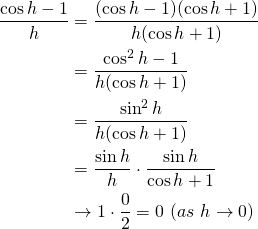
となるので、(2)および(3)より、
(4) ![]()
が得られました。
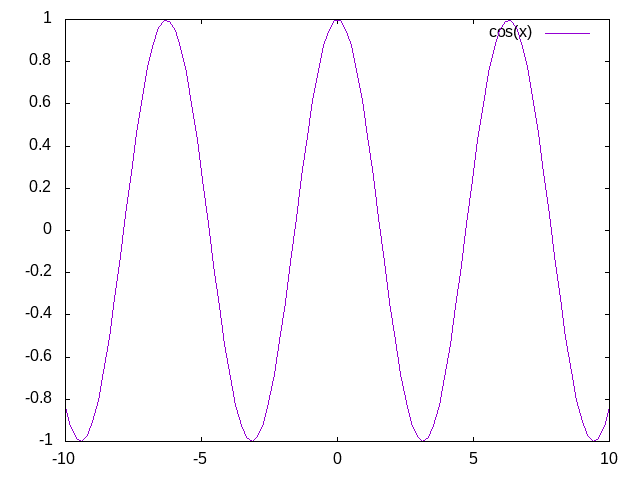
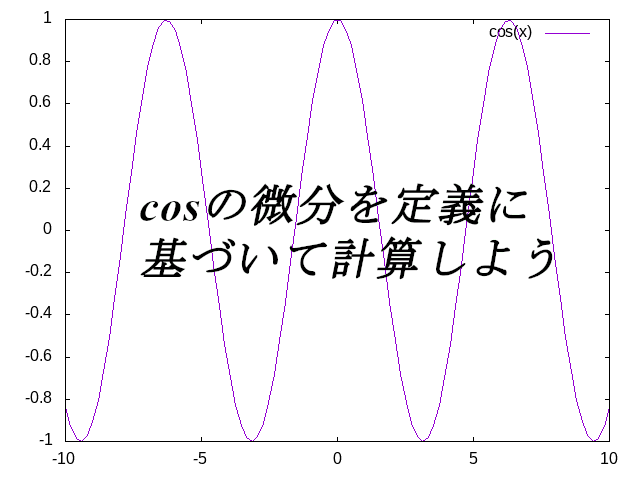
ちなみに![]() のグラフはこんな感じになります。
のグラフはこんな感じになります。
おわりに
というわけで今回は![]() の微分を定義に基づいて導きました。
の微分を定義に基づいて導きました。
改めて計算すると![]() の微分の時と同様、加法定理と
の微分の時と同様、加法定理と![]() の極限が非常に重要な役割を果たしていることがわかりますね。
の極限が非常に重要な役割を果たしていることがわかりますね。
実際、この二つはとても重要なのでどちらもよく理解しておきましょう。加法定理に関してはまだ当ブログでは解説していないので、いずれ解説出来たらなと思っています。
現状は自分の思いついた順で記事を書いていますが、数学に関してはある程度体系的にまとめたら自分の復習になるし、記事も読みやすくなるので、徐々にいろんな話題について書いていきたいですね。
ではまた。











コメント