どうもこんにちは。
突然ですが、「距離って何?」って聞かれたときに皆さんならどの様に答えるでしょうか?
というのも、ちょっと面白い(と自分では思っている)数学の小話として、色々な円を考えてみようという記事を書こうと思ってですね。
その前に距離とは何か?って話をする必要があるよな~と思ったのでこの記事を書き始めました。
距離の定義を与えて、さらに何種類かの距離を具体例として考えてみます。
普段何気なく使っている距離という概念ですが、改めて考えてみると楽しいかもしれませんよ!
という事で、早速距離について考えていきましょう!
距離の定義
距離の定義を与える前に、まずは言葉による説明を試みてみましょう。
距離とは、二点間の近さを測る何かしらの指標である。
こんな説明でどうでしょうか?
自分で書いといて言うのもあれですが、文学的すぎてちょっともやもやしますね。
そこでもう少し数学的な定義を与えてみます。
まず、![]() を集合として、次の条件を満たす距離関数
を集合として、次の条件を満たす距離関数![]() 考えます。
考えます。
その条件とは、![]() を
を![]() の任意の元として
の任意の元として
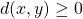
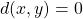 ならば
ならば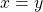
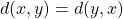
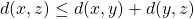
が成立することです。
これだけだとわかりづらいかもしれないので、言葉での説明もしてみますね。
まず距離関数![]() というのは、集合
というのは、集合![]() から2つ要素を受け取り実数を返すモノです。
から2つ要素を受け取り実数を返すモノです。
距離関数の条件の1つ目と2つ目は距離関数の値は必ず0以上になり、また0になるのは関数に入れた要素が同じであるときだけという事を主張しています。
次に3つ目は関数に入れる要素の順番は結果に影響しない事を主張しています。
最後に4つ目は三角不等式と呼ばれる性質で、ちょっとわかりづらいかもしれません。
イメージ的には「ある2点間を結んだ距離は別の点を経由した距離以下になる」といった感じです。
図で書くとこんな感じ。
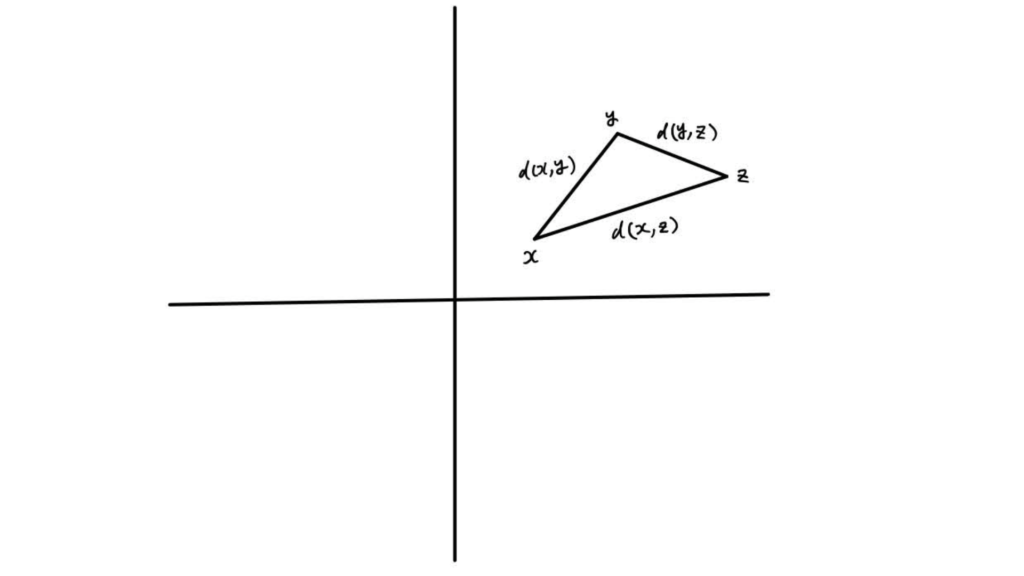
まさかの手書きですみません…。いつかちゃんとした図を描く…かもしれないです。
この図における集合![]() としては
としては![]() 、つまり通常の平面を考え、距離関数
、つまり通常の平面を考え、距離関数![]() としては2点を渡すとその2点間を結んだ長さを返す関数を考えています。
としては2点を渡すとその2点間を結んだ長さを返す関数を考えています。
この問題設定の場合は![]() であることは三角形の成立条件の1つにもなっています。これが三角不等式と言われる所以のはず。
であることは三角形の成立条件の1つにもなっています。これが三角不等式と言われる所以のはず。
そして、2点間に対する距離関数の値をその2点間の距離と呼ぶことにします。
この様に数学では、○○という条件を満たすものを△△と定義する、と言った定義の仕方を良くします。
慣れないとちょっとわかりづらいですが、抽象的に定義することで色々と拡張出来たり汎用性を持たせることができて何かと便利ですからね。
とはいえ、抽象的な定義だけでは理解しづらいのも事実なので、いくつか具体的な距離関数を実際に考えてみましょう。
距離の具体例1:ユークリッド距離
まずは、ユークリッド距離と呼ばれる距離を考えてみます。
特にここでは平面でのユークリッド距離を考察します。
まず集合![]() としては
としては![]() を考え、
を考え、![]() 上の点
上の点![]() は、
は、![]() と表されるとします。
と表されるとします。
ここで、![]() は共に実数で、それぞれ第一座標、第二座標と呼びます。
は共に実数で、それぞれ第一座標、第二座標と呼びます。
座標って何ぞやって話も出てきてしまいますが、それまで書いてしまうと長くなるので今回は省略。そもそも座標とはみたいな話をするのって結構難しいしね。
![]() と同様に
と同様に![]() も
も![]() と表されるとして、距離関数
と表されるとして、距離関数![]() を
を
![]()
により定義します。
この距離関数により測られる距離を平面におけるユークリッド距離と呼びます。
ここでは2次元平面を考えましたが、考える集合を変えることにより3次元空間でのユークリッド距離や、さらには![]() 次元空間におけるユークリッド距離なんかも考えることができます。
次元空間におけるユークリッド距離なんかも考えることができます。
また、この関数![]() が距離関数の条件を満たすことも証明できるので、興味がある方はやってみてください。
が距離関数の条件を満たすことも証明できるので、興味がある方はやってみてください。
距離の具体例その2:最大値normから誘導される距離
続いて、別の距離関数を考えていきます。
距離によく似た概念として、normというものがあって、それを用いても距離を定義することができて、実は先ほどのユークリッド距離も2-normから誘導される距離と考えることが出来ます。
ここでは特に最大値normから誘導される距離というものを考えてみます。なお、normとは何かという話は今度別の記事で書こうと思っているので、書けたらリンクを貼りますね。
先ほどと同様に、![]() として、
として、![]() の要素
の要素![]() が
が![]() と表されているとします。
と表されているとします。
この時、次の関数、
![]()
は距離関数になり、この関数により定まる距離を最大値normから誘導される距離と呼びます。
ここで縦棒は絶対値を表し、maxは大きい方を取り出す操作になります。
これまた図でちょっと説明してみますね。
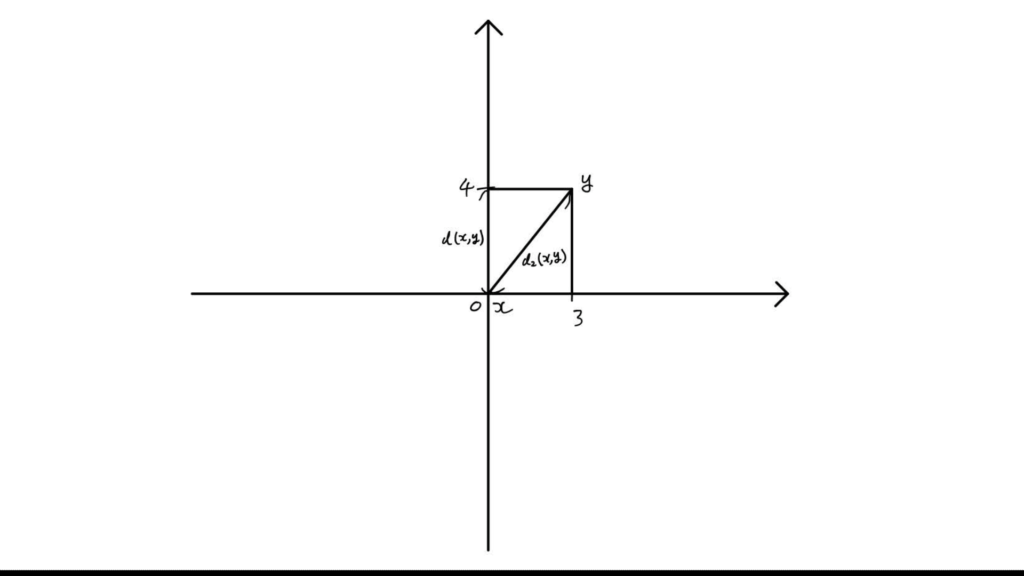
![]() とすると、先ほどのユークリッド距離では
とすると、先ほどのユークリッド距離では
![]()
となります。これは![]() と
と![]() を結ぶ最短距離で、通常の意味での距離になっていますね。図中の斜め線の長さです。
を結ぶ最短距離で、通常の意味での距離になっていますね。図中の斜め線の長さです。
一方、最大値normから誘導される距離はというと、
![]()
となります。
これは成分毎の差の絶対値の大きい方になっていますね。
この様に一口に距離と言っても、どの距離関数で測るかによって同じ点でも距離が変わってきます。
数学に慣れ親しんでる人にとっては当たり前の事なんですけど、ちょっと楽しくないですか?
自分はこういう話割と好きだったりします。
距離の具体例その3:離散的な距離
これまでは、距離を考える集合として連続的な集合を扱っていましたが、離散的な集合に対しても距離を導入することができます。
試しにアルファベット間に距離を導入してみましょう。
まず集合![]() として、次の集合
として、次の集合
![]()
を考えます。
さらに、![]() から
から![]() への関数
への関数![]() を
を
![]()
により定義します。
この時関数![]() の任意の元
の任意の元![]() に対して関数
に対して関数![]() を
を
![]()
により定義すると、これは距離関数の条件を満たします。
…実はこれ即興で作ってまだ証明していないので、もしかしたら満たさないかも。
もし満たさなかったらごめんね。てへぺろ。
ここで定義した関数![]() が距離関数になっているかはともかくとして、こんな感じで工夫してあげることで、一見距離を定義できなさそうな集合にも距離を入れることができます。
が距離関数になっているかはともかくとして、こんな感じで工夫してあげることで、一見距離を定義できなさそうな集合にも距離を入れることができます。
これが抽象的に定義しておいたことによる恩恵で、似たような話が色々とあります。
いつか似たような話として、抽象的に円、あるいは球を定義すると色々面白い話があるよって記事を書こうと思っているのでそちらもお楽しみに。
まとめ
という事で、抽象的に距離を定義して、その後具体的な距離をいくつか見てみました。
一口に距離って言っても、色々な測り方があるんだな~ってことが伝わり、少しでも楽しく感じてくれたら嬉しいです。
ではまた!











コメント