どうもこんばんは。最近生活リズムが崩壊しつつあるJrです。
朝早く起きる必要性がないと、どうしても夜遅くまで作業をしてしまって朝起きれないですねぇ…。
そういう意味でもやはり研究室に行って研究をするというのは大切かもしれないですね。
さて、最近テレビなどを観ていると、主にコロナに関する報道などで、指数関数的増大というワードを聞くことも多いかと思います。
でも中には、

指数関数的増大ってどのくらいの速さでの増大よ!
と思う方もいるかと思います。というか今日実際友人に聞かれました。
ということで、今日は指数関数について簡単に復習をしてみて、どのくらい増加のスピードが速いのか、その感覚をお伝えできればなと思います。
指数関数の定義
指数関数、特にネイピア数![]() を底とする指数関数は以下により定義されます。
を底とする指数関数は以下により定義されます。
(1) ![]()
底は「そこ」ではなく「てい」と読みます。
底は必ずしも![]() である必要はなく、
である必要はなく、
(2) ![]()
を満たす実数であればなんでもいいです。
もちろん、底としてどんな実数を用いるかにより、関数値自体は変わるのですが、関数の大まかな振る舞いは
の二通りに分類されます。
1.の時は、![]() が大きくなると関数値は(単調に)減少し、2.の時は
が大きくなると関数値は(単調に)減少し、2.の時は![]() が大きくなると関数値が(単調に)増加します。
が大きくなると関数値が(単調に)増加します。
単に指数関数といったときには、底をネイピア数とする指数関数を指す場合が多いので、本記事でも底をネイピア数とする指数関数を扱うこととします。
なお、ネイピア数は
(3) ![]()
により定義される無限小数で、![]() と続きます。
と続きます。
よって、![]() なので
なので![]() は単調増加の関数となります。
は単調増加の関数となります。
ネイピア数に関する話も色々書けるとは思うのですが、今回の話題からは脱線してしまうのでまた別の記事で…。
他の関数との比較:一次関数、二次関数を例に
さて、指数関数の定義を確認したところで、こいつがどんな挙動をするのかを眺めてみましょう。
挙動の理解を深めるために、
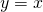 (一次関数)
(一次関数)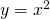 (二次関数)
(二次関数) (指数関数)
(指数関数)
と三種類のグラフを書いて比較してみたいと思います。
グラフを書いて挙動を眺めてみるのは、直感的な理解を助ける方法として非常に優れています。
まずは一次関数のグラフから見てみましょう

皆さんお馴染みの一次関数のグラフです。比例とも言いますね。![]() の値を定数倍(この場合は1倍)した値が関数値となります。
の値を定数倍(この場合は1倍)した値が関数値となります。
これだけ見ても何もわからないので、次は二次関数のグラフを見てみましょう。

二次関数というと放物線を思い浮かべる人が多いと思うので、描画範囲を![]() としました。
としました。
二次関数では![]() の値の二乗を定数倍した値(この場合は1倍)が関数値となります。
の値の二乗を定数倍した値(この場合は1倍)が関数値となります。
定義、およびグラフから![]() が大きくなると一次関数と二次関数の関数値の差が開いていくのがわかると思います。
が大きくなると一次関数と二次関数の関数値の差が開いていくのがわかると思います。
例えば![]() のときは、一次関数の関数値が2、二次関数の関数値が4であるのに対し、
のときは、一次関数の関数値が2、二次関数の関数値が4であるのに対し、![]() のときは一次関数の関数値が10、二次関数の関数値が100と、関数値の差が開いていますね。
のときは一次関数の関数値が10、二次関数の関数値が100と、関数値の差が開いていますね。
このことから、二次関数の方が増加率が大きいということがわかります。
増加率に関しては微分をすることでもわかるのですが今回の記事では触れないでおきます。
さて、いよいよ指数関数のグラフを見てみましょう。
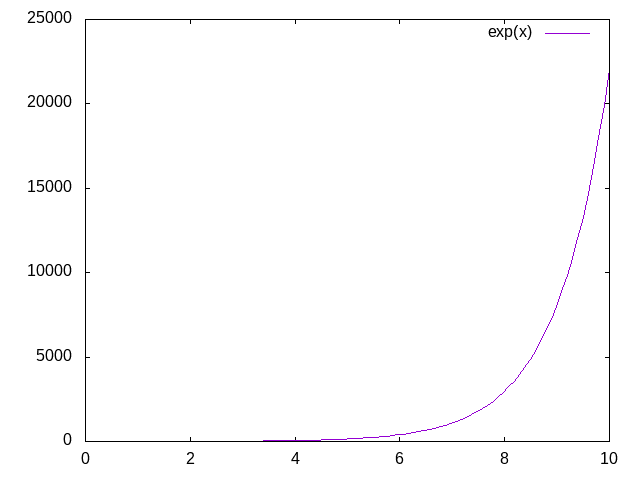
うん、増加の仕方がえげつないのがわかりますね。
![]() のときの関数値が25000て…。一次や二次とは文字通り桁が違いますね。
のときの関数値が25000て…。一次や二次とは文字通り桁が違いますね。
しかも実は![]() が大きくなると増加率がどんどん大きくなります。
が大きくなると増加率がどんどん大きくなります。
指数関数的増大とは
これまで見てきた通り、指数関数は一次関数や二次関数(実はもっと一般に多項式)と比較したときに、増加率が比較にならないほど大きいです。
ここで、変数![]() が日にちを、関数値が感染症の患者数を表すとします。
が日にちを、関数値が感染症の患者数を表すとします。
そして仮に感染者が指数関数にしたがって増加するとします。すると日数が経った後にどうなるかというと…。
めちゃくちゃやばいですよね。感染者の数がとんでもないことになります。
と、言うことで指数関数的増大とはものすごいレートで増大することを意味しています。
もちろん、感染症なんかは様々な要因で感染するので完全に指数関数にしたがうわけではないと思いますけど、指数関数的に感染者が増大しているというのは結構まずい状況なのかなぁと思います。
おわりに
今回は最近よく聞く指数関数的増大とはどんな増大なのかをグラフを交えながら解説してみました。
少しでも理解の助けになったなら幸いです。
ではまた別の記事でお会いしましょう。










コメント